在神经元中添加激活函数的原因？

因为很多数据不是线性可分的，如下第二张图

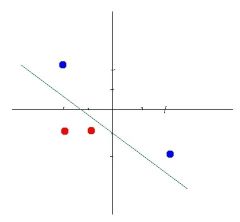
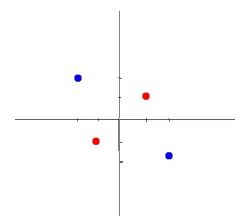
当数据不是线性可分时，就不能使用线性函数作为神经网络的输出，通常解决办法有两个：

1.做线性变换

2.引入非线性函数

线性变换

值 x, y 变成: x^2, y^2

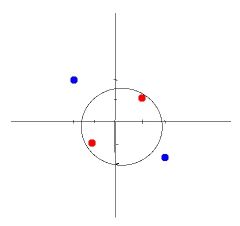
坐标轴 x, y 变成: x^2, y^2

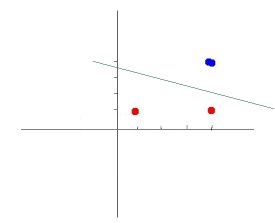
以上办法始终都是线性变换（矩阵换维）

有些问题，引入再多神经元，也是无法实现的。（线性变换只能做线性拼接）

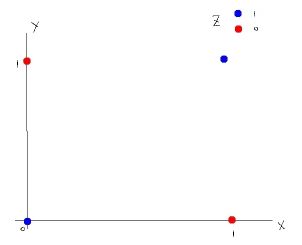
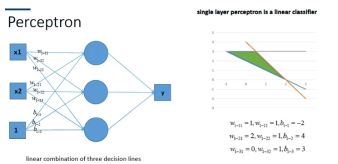
其他方面，线性变换计算成本很高，特定问题需要用特定的线性变换。

因此，普遍是在神经元中添加非线性函数

非线性

原则上可以是任何函数，只要是非线性的：Sigmoid, Tanh, ReLU, Leaky ReLU, Softmax, Binary step, Identity, Swish ... ...

实战经验就是试出来的。

其他

输入层不使用激活函数，激活函数一般作用域隐藏层，输出层可选择是否使用激活函数。有些激活函数只适合作用于隐藏层，有些只适合输出层。

不同层有时使用不同的激活函数。例如：输出层可以根据要解决的问题类型，单独使用某种激活函数。

线性非线性问题：有些神经网络中也使用线性激活函数。例如：回归问题神经网络。（没细研究）

函数选择要尽量简单，避免大量计算。

梯度

用通俗的语言讲梯度：瞎子下山，如何找到最优路径？每一步都走最陡的坡，当接近坡底时，开始走小碎步。

对应机器学习，就是目标值与预测值之间的差距。通过导函数计算出梯度，同时根据梯度及误差大小调整下降率。迭代进行。

梯度消失和梯度爆炸

为什么会产生梯度消失和梯度爆炸？

神经网络训练的方法都是根据损失函数计算误差，通过梯度反向传播的方式，指导深度网络权值的更新优化。 其中将误差从末层往前传递的过程需要链式法则（Chain Rule）的帮助，因此反向传播算法可以说是梯度下降在链式法则中的应用。 而链式法则是一个连乘的形式，所以当层数越深的时候，梯度将以指数形式传播。 梯度消失问题和梯度爆炸问题一般随着网络层数的增加会变得越来越明显。 在根据损失函数计算的误差通过梯度反向传播的方式对深度网络权值进行更新时，得到的梯度值接近0或特别大，也就是梯度消失或爆炸。 梯度消失或梯度爆炸在本质原理上其实是一样的。

【梯度消失】 一是在深层网络中，二是采用了不合适的损失函数，比如sigmoid。 当梯度消失发生时，接近于输出层的隐藏层由于其梯度相对正常，所以权值更新时也就相对正常，但是当越靠近输入层时，由于梯度消失现象，会导致靠近输入层的隐藏层权值更新缓慢或者更新停滞。 这就导致在训练时，只等价于后面几层的浅层网络的学习。

【梯度爆炸】 一般出现在深层网络和权值初始化值太大的情况下。在深层神经网络或循环神经网络中，误差的梯度可在更新中累积相乘。 如果网络层之间的梯度值大于 1.0，那么重复相乘会导致梯度呈指数级增长，梯度变的非常大，然后导致网络权重的大幅更新，并因此使网络变得不稳定。

梯度爆炸会伴随一些细微的信号，如： ①模型不稳定，导致更新过程中的损失出现显著变化； ②训练过程中，在极端情况下，权重的值变得非常大，以至于溢出，导致模型损失变成 NaN等等。

Loss function（损失函数）

（本例源码里面叫 errorFunction ）

用来估量模型的预测值f(x)与真实值Y的不一致程度，通常是一个非负实值函数。

损失函数有很多种类型。

bias（偏置）

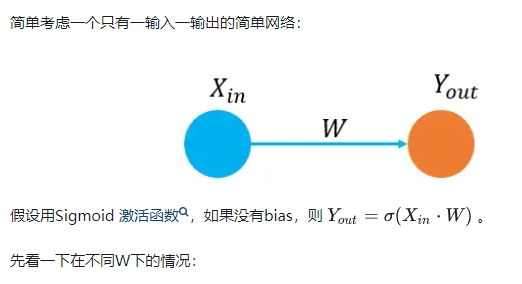
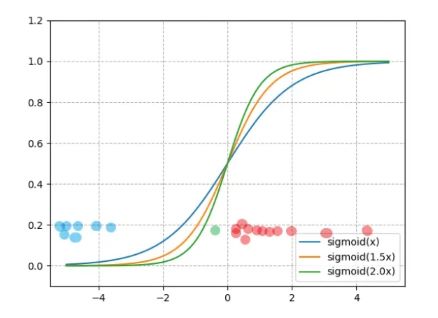
假如输入 X 的输入分布如图中蓝点（A集合）和红点（B集合）所示，要通过 Y ( > 0.5 or < 0.5，用 y = 0.5 分类) 来判断输入时在A内还是B内，很显然，要提高准确性，sigmoid 函数中的 W 系数需要学的很大，才能保证尽可能的判断准确。

但是如果一个测试样本在图中绿点所在的位置，很明显我们（人）可以将绿点判为红点所在的B集合， 但是通过训练学到的 W 是不能正确判断的（因为 绿点的 Y 值 < 0.5）。这个时候似乎让soigmoid函数变得更陡也没法解决了。

但是如果加一个bias呢。

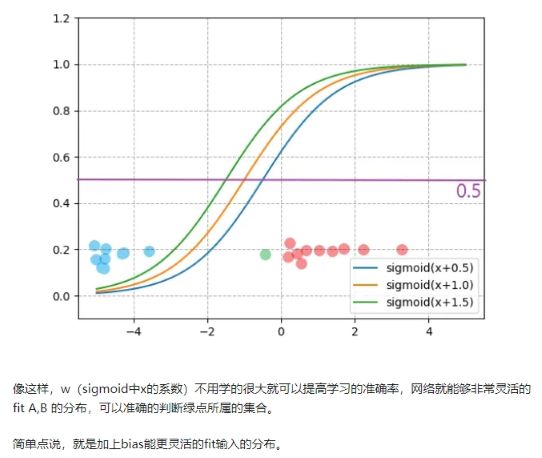
【加了偏置拟合不是经过原点的分布】 偏置 b 在网络中的目的是使得当某一层layer的输入分布不是0为中心时给予偏置补偿（比如简单来看，要拟合 y=wx+b，b=100，那么用没有偏置的单层网络y=wx是怎么都无法拟合的！） 但是，当该层layer的输入经过归一化，也就是0为中心时，不要偏置也可以拟合（对应上述的例子，就是把所有数据移到原点附近，这时候y=wx就能拟合，拟合方向就行）通常情况下我们拿到的数据都不是0中心分布的，所以需要偏置b。

【偏置可以加速神经网络拟合】 加个偏置b 其实也可以看作是每个神经元多了个参数w0 * x0 （x0取值为1）。

Learning rate （学习率）

学习率就是每次参数更新的行进步长。

步长过大则有可能越过了最优解，反复横跳不能得到最优效果。步长过小则不仅收敛效果慢，还有可能如下图一样陷入局部最优，这时候加大学习率才能越过山头找到真正的最优解。

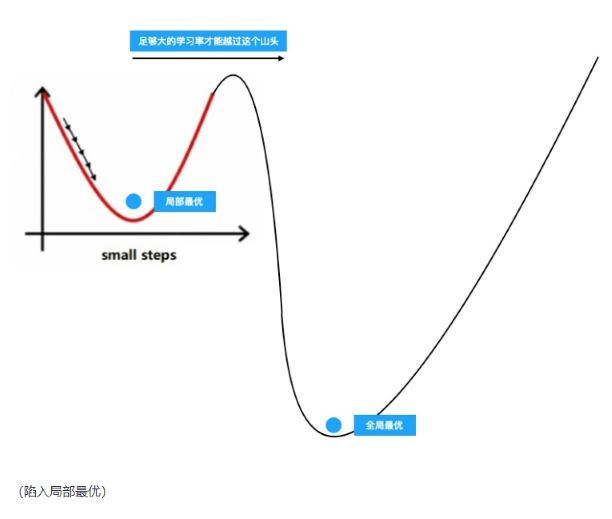
不同的模型也有不同的合适学习率可选择。甚至你可以用一些动态学习率的方法来在运算的过程中动态调整学习率，loss 下降明显时加大学习率，loss 趋缓时减小学习率。

本例使用固定学习率，但步长实际上也是动态的，因为会叠加误差导数，随着正确结果的逼近，误差会越来越小。

Regularization（正则化）

正则化这个翻译感觉不准确，可以理解成“约束”。主要用途是解决 过拟合。

本例有两种 L1 L2

L1 范数：权值向量 w 中各个元素的绝对值之和。

L2 范数：权值向量 w 中各个元素的平方和求平方根。

不管是传统机器学习模型，还是深度学习模型，训练过程中都有越来越贴近训练数据的趋势，越贴近训练数据，在其他的预测数据上就越容易犯错，也就是过拟合。模型越复杂，越容易过拟合。regularization就是要限制模型的这个缺陷，有的是在模型设计阶段的regularization，有的是在模型训练阶段的regularization，目的都是防止过拟合。

Regularization rate（正则化率）：正则化计算结果的系数。

问题类型（Problem type）

本例都是介绍的分类问题，目的是给定一个数据，通过神经网络预测它属于哪个类别。

另一种问题类型叫回归问题，给定一个数据，通过神经网络预测它的数值。